This post is written in Chinese. Please consider using Google Translate

[有向树] 一个弱连通有向图，若去掉方向后得到一棵树，则称此有向图为一棵有向树，记为T。

[外向树] 若一个有向树T，有且只有一个顶点入度为0，其余顶点入度都为1，则称T为外向树。T中入度为0的节点被称为T的根节点，出度为0的节点被称为T的叶节点。每个节点的有向边指向的节点被称为该节点的子节点。

[内向树] 若一个有向树T，有且只有一个顶点出度为0，其余顶点出度都为1，则称T为内向树。T中出度为0的节点被称为T的根节点，入度为0的节点被称为T的叶节点。每个节点的有向边的反向边指向的节点被称为该节点的子节点。

外向树和内向树都是有根树。

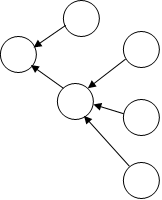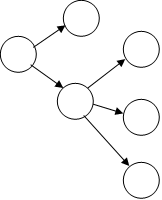
图1	图2

如上，图1为一棵外向树，图2为一棵内向树。

[树的括号序列最小表示法]

定义S[t]表示以t为根的子树的括号序列

S[t]=

{

'(',')' (如果t为叶节点)

'(',S[c1],S[c2],...,S[ck],')' (c1,c2,...,ck为t的k个子节点，S[c1],S[c2],...,S[ck]要按照字典序排列)

}

为了保证同构的树的括号序列表示具有唯一性，我们必须规定子树点的顺序。按照子树的括号序列的字典序就是一种不错的方法。

例如上述图2，它的括号序列最小表示就是((()()())())。

[有根树的同构]

对于一个有根树，我们可以通过比较他们的括号序列的最小表示，如果他们的括号序列最小表示完全相等，那么他们同构。

BYVoid 原创讲解，转载请注明。