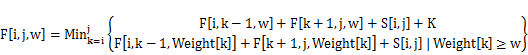NOI 2009 二叉查找樹

問題簡述

有一棵Treap，每個節點有一個互不相同的數據值和權值，以及一個訪問頻度。一個節點的訪問代價爲它的訪問頻度乘以它在樹中的深度，整棵樹的訪問代價定義爲所有節點的訪問代價之和。節點的權值可以修改爲任意實數，每修改一個節點的權值的代價爲K。任務是修改一些節點的權值，使得整棵樹的訪問代價與修改代價之和最小。

問題建模

首先離散化所有節點的權值，對所有節點按照數據值排序後線性存儲。定義S[i,j]爲(排序後)第i個節點到第j個節點的訪問頻度之和。

解法 動態規劃

算法描述
定義Weight[i]爲狀態轉移方程爲第i個節點離散化後的權值，F[i,j,w]表示從第i個節點到第j個節點組成一棵子樹的最小代價，子樹根節點的權值≥w。狀態轉移方程爲

clip_image002

邊界條件爲clip_image004，目標函數爲clip_image006。

算法分析
對於一個狀態F[i,j,w]，我們要枚舉從節點[i..j]組成的這棵子樹的根節點k，其左子樹爲[i..k-1]，右子樹爲[k+1..j]。

如果根節點k的權值Weight[k]≥w，那麼節點k的權值無需修改即可直接作爲該子樹的根節點。總代價爲左子樹的代價F[i,k-1, Weight[k]]，加上右子樹的代價F[k+1,j, Weight[k]]，以及整個子樹的訪問頻度之和。

另外一種情況，修改節點k的權值，使之不小於w。由於我們已經離散化了權值，修改後的權值不應是整數，以免和已有重複。假設節點k修改後的權值爲w加上一個很小的小數，其左右子樹根節點的權值都不應小於節點k修改後的權值。我們約定如果根和子節點都必須大於w的話，則子節點的權值比根節點略大，且大於w。於是這種情況的總代價爲左子樹的代價F[i,k-1, w]，加上右子樹的代價F[k+1,j, w]，加上修改權值的代價K，以及整個子樹的訪問頻度之和。

複雜度分析
狀態數爲O(N3)，每次轉移需要以O(N)的時間枚舉k，所以時間複雜度爲O(N4)。在實際測試中通過了所以測試點，得到100分。

參考程序

/* 
 * Problem: NOI2009 treapmod
 * Author: Guo Jiabao
 * Time: 2009.9.24 14:50
 * State: Solved
 * Memo: 動態規劃
*/
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
using namespace std;

typedef long long big;

const int MAXN = 72;
const big INF = ~0ULL>>1;

struct node
{
    int val,wei,freq;
}P[MAXN];

int N,K;
big sf[MAXN],F[MAXN][MAXN][MAXN],Ans=INF;

void init()
{
    int i;
    freopen("treapmod.in","r",stdin);
    freopen("treapmod.out","w",stdout);
    scanf("%d%d",&N,&K);
    for (i=1;i<=N;i++)
        scanf("%d",&P[i].val);
    for (i=1;i<=N;i++)
        scanf("%d",&P[i].wei);
    for (i=1;i<=N;i++)
        scanf("%d",&P[i].freq);
    memset(F,-1,sizeof(F));
}

inline int cmp1(const void *a,const void *b)
{
    return ((node *)a) -> wei - ((node *)b) -> wei;
}

inline int cmp2(const void *a,const void *b)
{
    return ((node *)a) -> val - ((node *)b) -> val;
}

inline big sum(int i,int j)
{
    return sf[j] - sf[i-1];
}

big dp(int i,int j,int w)
{
    if (i>j)
        return 0;
    if (F[i][j][w] == -1)
    {
        int a;
        big t,rs=INF;
        for (a=i;a<=j;a++)
        {
            t = dp(i,a-1,w) + dp(a+1,j,w) + sum(i,j) + K;
            if (t < rs)
                rs = t;
            if (P[a].wei >= w)
            {
                t = dp(i,a-1,P[a].wei) + dp(a+1,j,P[a].wei) + sum(i,j);
                if (t < rs)
                    rs = t;
            }
        }
        F[i][j][w] = rs;
    }
    return F[i][j][w];
}

void solve()
{
    int i;
    qsort(P+1,N,sizeof(P[0]),cmp1);
    for (i=1;i<=N;i++)
        P[i].wei = i;
    qsort(P+1,N,sizeof(P[0]),cmp2);
    for (i=1;i<=N;i++)
    {
        P[i].val = i;
        sf[i] = sf[i-1] + P[i].freq;
    }
    for (i=0;i<=1;i++)
    {
        big t = dp(1,N,i);
        if (t < Ans)
            Ans = t;
    }
}

int main()
{
    init();
    solve();
    cout << Ans << endl;
    return 0;
}

相關日誌